降维方法小结

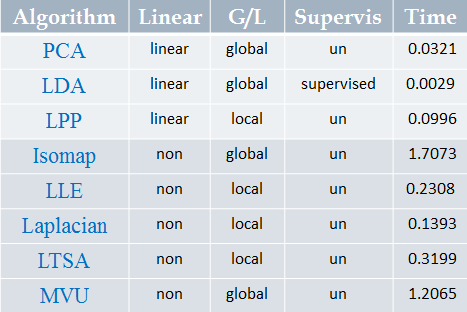
数据降维分类

传统线性方法

PCA

PCA 见前文 ### ICA独立成分分析 PCA 主要针对高斯噪声的数据， ICA 可以不需要知道分布 ICA又称盲源分离(Blind source separation, BSS),它假设观察到的随机信号x服从模型\(x=As\)，其中s为未知源信号，其分量相互独立，A为一未知混合矩阵。ICA的目的是通过且仅通过观察x来估计混合矩阵A以及源信号s。cite eg：经典鸡尾酒宴会问题 调整到zero means \[x = As \rightarrow \sum_i^na_is_i\] \[求解：s = A^{-1}x = Wx\] 下面问题在于如何计算W，方法是用极大似然估计 给数据分布做出假设，一般假设sigmoid函数为pdf 假设分量独立，联合分布概率密度$p(s) = _i^n p_s(s_i) $ \[p(x) = p_s(Wx)|W| = |W|\prod_i^n p_s(w_i^Tx)\] \[l(W) = \sum_{i=1}^m\sum_{j=1}^nlog(p_s(w_j^Tx^{(i)}+log|W|))\] 求导求解 参考资料： 参考文献 博客

LDA (Linear discriminant analysis)

目标：使用这种方法能够使投影后模式样本的类间散布矩阵最大，并且同时类内散布矩阵最小 两类的均值向量\(m_1,m_2\) 最大化类间差距 \(d_{12} = m_2 - m_1 = w^T(n_2-n_1)\) 最小化类内方差 \(s_k^2 = \sum_{n \in C_k}(y_n-m_k)^2, y_n = w^Tx_n\) 优化目标 $J(w) = $ 定义类间方差$ S_B = (m_2-m_1)(m_2-m_1)^T $ 类内方差$ S_W = S_{w1} + S_{w2}$ 则目标函数变成： \[ J(w) = \frac{w^TS_Bw}{w^TS_Ww}\] 方法1：Lagrange法 \[min: J(w) = w^TS_Bw-\lambda (w^TS_Ww-1)\] \[求导得 S_Bw = \lambda S_Ww\] \[J(w) = \lambda\] 而\(\lambda\)的最大值即\(S_W^{-1}S_B\)的最大特征值，\(w\)为对应特征向量

方法2：坐标变换 \(S_W = L^TL,z = Lw\) 则不失一般性\(||z||_2 = 1\), \(J(w) = z^TL^{-T}S_WL^{-1}z\) 略

流形学习

“天地有正气，杂然赋流形” – 文天祥 资料： 何晓飞ppt，pluskid博文

MDS (Multiple Dimensional Scaling, 多维缩放)

要求原始空间中样本的距离在低维空间得以保持 假定m个样本在原始样本空间\(\mathbb{R}^d\)的距离为\(D\in \mathbb{R}^{m\times m}\) 要获得低维空间表示\(Z = \mathbb{R}^{d'\times m}\) 令低维空间内积矩阵为\(B = Z^TZ\in \mathbb{R}^{m\times m}\) 其中\(b_{ij}=z_i^Tz_j\),则\(d_{ij}^2=b_{ii}+b_{jj}-2b_{ij}\) 令降维后样本Z中心化，\(\sum_{i=0}^mz_i=0\) 经过推导，可得\(b_{ij}=-\frac{1}{2}(d_{ij}^2-d_{i\cdot}^2-d_{\cdot j}^2+dist_{\cdot\cdot}^2)\) 即矩阵\(B\)可以通过原始数据的距离算出，详见西瓜书p228 对\(B\)做特征值分解，再选取主成分，可以求得\(Z\)，即得到降维的表示

Isomap (等度量映射)

Isomap 简单讲一下 Isomap 是按照测地线的距离去算两点间的距离，再用MDS降维

LLE（Locally linear embedding）

与Isomap不同，LLE试图保持邻域内的样本之间的线性关系 \[x_i \approx \sum_{j=1}^kw_{ij}x_j,k个足够近的点线性表示\] \[\min_{w} \sum_{i=1}^m||x_i-\sum_{j\in Q_i}w_{ij}x_j||_2^2\\ s.t. \sum_{j\in Q_i}w_{ij} = 1 \] 求解\(w\)是一个投影问题 求出\(w\)后，LLE可以表示为 \[\min_{z_i}\sum_{i=1}^m||z_i-\sum_{j\in Q_i}w_{ij}z_j||_2^2\] 其中\(z_i\)为\(x_i\)对应的低维表示 令\(Z = (z_1,z_2,\cdots,z_m)\in \mathbb{R}^{d'\times n}, (W)_{ij} = w_{ij}\) 则优化目标可以写成 \[\min_{Z}tr(ZMZ^T)\\ s.t. ZZ^T = I\\ 其中 M = (I-W)^T(I-W) \] 可以看出该问题即求解M的\(d'\)个最小特征值对应的特征向量\(z\)

参考资料: 论文 、tutorial

Isomap 与 LLE 效果比较

LE (Laplacian Eigenmaps, 拉普拉斯特征映射)

Step 1 (constructing the adjacency graph). We put an edge between nodes i and j if xi and xj are “close.” - neibours - knn

Step 2 (choosing the weights).1 Here as well, we have two variations for weighting the edges: - Heat kernel \(W_{ij} = e^{-||x_i-x_j||^2/t}\)if connected - binary 0/1

Step 3 (eigenmaps). Compute eigenvalues and eigenvectors for the generalized eigenvector problem \(Lf = \lambda Df\) , where \(D_ii = \sum_jW_{ji}, L=D-W\) \[0 = \lambda_0\le \lambda_1\le\cdots\le\lambda_{k-1},对应解向量f_0,f_1,\cdots,f_{k-1}\] for embedding in m-dimensional Euclidean space: \[x_i\rightarrow(f_1(i),\cdots,f_m(i))\]

算法解释 有了相似度矩阵\(W\)后，目标就可以刻画为 \[l(W) = \sum_{ij}(y_i-y_j)^2W_{ij}\\ 又\sum_{ij}(y_i-y_j)^2W_{ij} = \sum_{ij}(y_i^2+y_j^2-2y_iy_j)W_{ij}\\ =\sum y_i^2D_{ii}+\sum_jy_j^2D_{jj}-2\sum_{ij}y_iy_jW_{ij}\\ = 2y^TLy \] 则问题转化为\[\min_y y^TLy, \ \ s.t. y^TDy=1 \] 对于所有\(y\),\[\min_Y tr(Y^TLY), \ \ s.t. Y^TDY=I\] constraint 解释： > The constraint yTDy = 1 removes an arbitrary scaling factor in the embedding. Matrix D provides a natural measure on the vertices of the graph.The bigger the value Dii (corresponding to the ith vertex) is, the more “important” is that vertex.

puskid 博客上说了一句，还没理解 > 实际上，从理论上也可以得出二者之间的联系, LE 对应于\(L\),而 LLE 对应于 \(L^2\)

参考资料: 博客 ### LPP (Locality Preserving Projection),局部保留投影.Xiaofei He 2999

It builds a graph incorporating neighborhood information of the data set algorithm： 1. Constructing the adjacency graph: Let G denote a graph with m nodes. We put an edge between nodes i and j if xi and xj are ”close”. a.Euclidean b.knn 2. Choosing the weights: W is a sparse symmetric m × m matrix with Wij having the weight of the edge joining vertices i and j, and 0 if there is no such edge. a.Heat kernel b.binary 3. Eigenmaps: Compute the eigenvectors and eigenvalues for the generalized eigenvector problem:\[XLX^Ta = \lambda XDX^Ta\] D is a diagonal matrix w, \(D_{ii} = \sum_j W_{ji}\) , \(L = D-W\) is the laplacian matrix, the ith column of \(X\) is \(x_i\) \[x\rightarrow y=A^Tx, A = (a_0,a_1,\cdots,a_{l-1})\]

从算法过程来看，LPP与LE极其相似 在 LPP 中，降维函数跟 PCA中一样被定为是一个线性变换，用一个降维矩阵 A 来表示，于是 LE 的目标函数变为 \[\sum_{i,j}(A^Tx_i-A^Tx_j)^2W_{ij}\] 经过类似的变换以后，得到类似的特向量问题 \[XLX^Ta = \lambda XDX^Ta\]

参考资料: pluskid博客 论文