马尔可夫决策 MDP
马尔可夫过程可以用一个五元数\((S, A, P(\cdot,\cdot), R(\cdot,\cdot), \gamma)\)
- S 是一组有限的状态集
- A 是一组有限的动作集
- \(P_a(s,s′)=Pr(s_{t+1}=s′|s_t=s,a_t=a)\) 表示在时间 t 状态 s 采取动作 a 可以在时间 t+1 转换到状态 s′ 概率
- \(R_a(s,s′)\) 表示通过动作 a 状态从 s 转换到 s′ 所带来的及时收益（或者是预期及时收益）
- \(\gamma \in [0,1]\) 是折扣因子(discount factor)，表示未来收益和当前收益之前的差别
目标寻找策略\(\pi(s): S \rightarrow A\)最大化累计收益R(T) \[ R(T) = \sum_{t=1}^{T} \gamma^tR_{a_t}(s_t, s_{t+1}) \]
Bellman Equation
\[ v_\pi(s) = \sum_{a \in A}\pi(a|s)(R_s^a + \gamma\sum_{s'\in S}P_a(s,s')v_\pi(s')) \\ v_\pi = R^\pi + \gamma P^\pi R^\pi \\ v_\pi = (I - \gamma P^\pi )^{-1}R^\pi \]
多臂老虎机 (Multi-Armed Bandit)
老虎机有一个绰号叫单臂强盗（single-armed bandit）。假设面对一排期望收益不同得老虎机，你采取什么策略来保证总收益最高？这就是经典的多臂老虎机问题。
问题描述
\(A: \text{set of actions(arms)}\)
\(R^a(r) = P[r|a]: \text{unknown probability distribution over rewards}\)
目标是最大化累计收益 \[ \sum_{\tau=1}^t r_\tau \\r_t \sim R^{a_t}, a_t \in A \] 定义后悔
每次action的平均收益是\(Q(a) = \mathbb{E}[r|a]\)，最优值\(V^* = Q(a^*) = max_{a \in A} Q(a)\)
regret \(l_t = \mathbb{E}[V^* - Q(a_t)]\)
总regret \[ L_t = \mathbb{E}[\sum_{\tau =1}^tV^* - Q(a_\tau)] \\ = \sum_{a \in A}\mathbb{E}[N_t(a)](V^*-Q(a)) \\ = \sum_{a \in A}\mathbb{E}[N_t(a)]\Delta_a \]
Exploitation & Exploration
（1）Exploitation：基于已知最好策略，开发利用已知具有较高回报的item（贪婪、短期回报）
- Advantage：充分利用已知高回报item
- Disadvantage：陷于局部最优，错过潜在更高回报item的机会
（2）Exploration：不考虑曾经的经验，勘探潜在可能高回报的item（非贪婪、长期回报）
- Advantage：发现更好回报的item
- Disadvantage：充分利用已有高回报item机会减少（如已经找到最好item）
（3）目标：要找到Exploitation & Exploration的trade-off，以达到累计回报最大化
一直exploit和永不exploit都是线性的regret，如何找到更优的策略
\(\epsilon\)-greedy算法
分配一定概率去explore
算法特点
- 如果item的回报发生变化，能及时改变策略
- 可以控制\(\epsilon\)对Exploration和Exploitation的偏好程度，但是\(\epsilon\)难以选择
- 策略运行一段时间后，我们对item的好坏了解的确定性增强，但仍然花费固定的精力和随机策略去exploration
算法改进
- ε-first strategy，一开始分配部分explore
- ε-decreasing strategy，随着时间减小explore
- softmax，改变随机选择策略，分配概率
UCB（Upper Confidence Bound）算法
根据以下策略选择action \[
a_t = \arg\max_{a\in A}~ \hat{Q_t}(a) + \hat{U_t}(a)
\] 
\[
P[Q(a) > \hat{Q_t}(a) + U_t(a)] \le e^{-2N_t(a)U_t(a)^2} = p
\]
UCB1算法
令\(p = t^{-c}\), e.g c = 4，\(U_t(a) = \sqrt {\frac{2\log t}{N_t(a)}}\)
\[ a_t = \arg\max_{a\in A} Q(a) + \sqrt {\frac{2\log t}{N_t(a)}} \]
UCB1 算法有logarithmic 的\(L_t\) 渐进
其它：UCB2，LinUCB
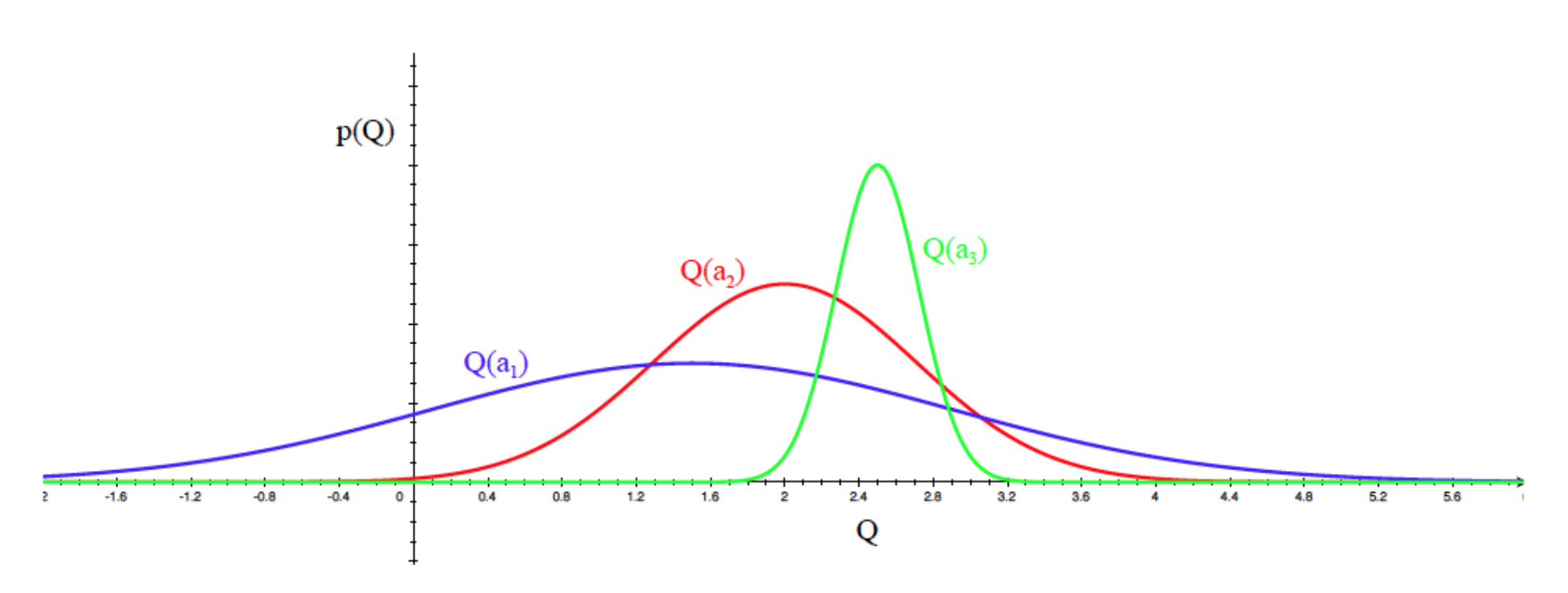
Bayesian UCB
假设高斯分布
\[
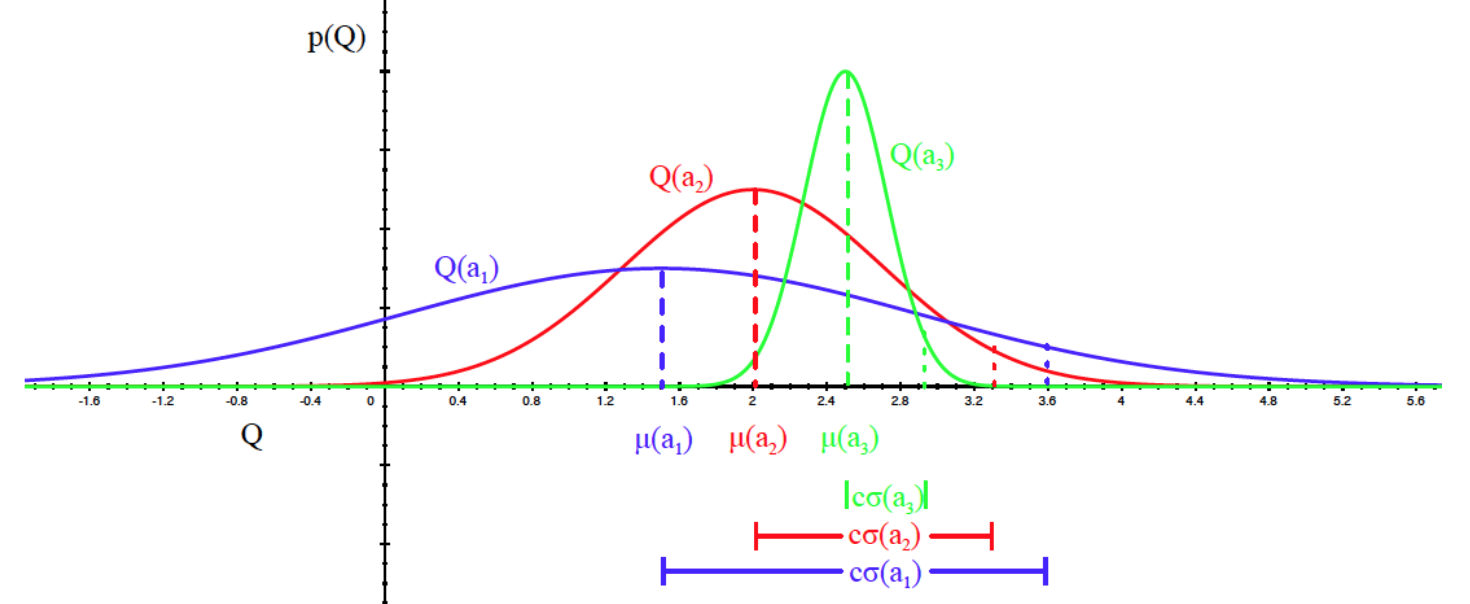a_t = \arg\max_{a\in A} \mu_a + c\sigma_a/\sqrt {N_t(a)}
\] 算法特点
- 考虑了回报均值的不确定性，让新的item更快得到尝试机会，将探索+开发融为一体
- 不需要设置参数
- 一开始各item选择次数都比较少，导致得到的回报波动较大，而且会尝试所有的选择
Thompson Sampling
Thompson 采样和贪心法的区别相当于频率学派和贝叶斯学派的区别
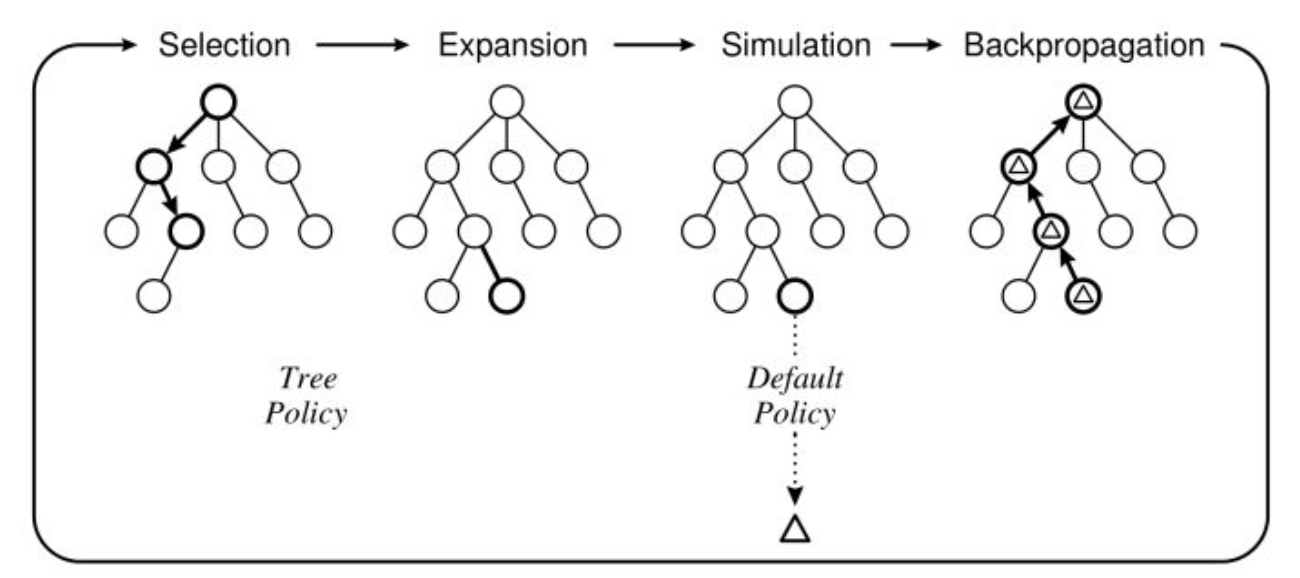
蒙特卡洛搜索树 MCTS
MCTS的四个基本过程：选择、扩展、仿真、反向传播。
参考资料
老虎机：https://www.zhihu.com/question/53381093
bandit算法：https://blog.csdn.net/legendavid/article/details/64439174
http://www.cs.cmu.edu/~rsalakhu/10703/Lecture_Exploration.pdf
极大极小算法：https://www.zhihu.com/question/27221568/answer/140874499
MDP:https://blog.csdn.net/WangJiankun_ls/article/details/70885008
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MDP.pdf
https://engineering.purdue.edu/~givan/talks/mdp-tutorial.pdf
Thampson Sampling: https://web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf
AlphaGo: http://science.npa.farbox.com/post/alphago/gou-jian-zi-ji-de-alphago